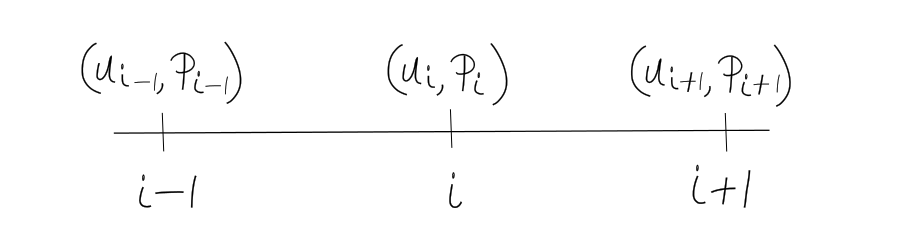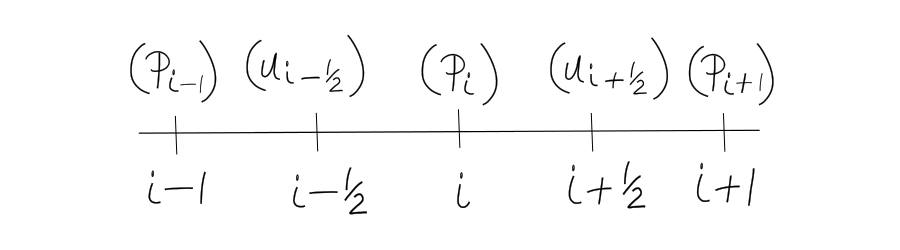1.1.4.2. The Marker and Cell Method

1.1.4.2.1. Collocated vs. Staggered Grids

  • Illustration: consider a 1D Navier-Stokes System

(1)\[{\partial u \over \partial x} = 0\]
(2)\[{\partial u \over \partial t} + {\partial u^2 \over \partial x} = - {1 \over \rho} {\partial p \over \partial x} + \nu {\partial^2 u \over \partial x^2}\]

  • On a standard collocated grid we have the following with FTCS:

(3)\[{{u_{i+1}^{n+1} - u_{i-1}^{n+1}} \over {2 \Delta x}} = 0\]
(4)\[{{u_{i}^{n+1} - u_{i}^{n}} \over {\Delta t}} + {({u_{i+1}^{n})^2 - (u_{i-1}^{n})^2} \over {2 \Delta x}} = - {1 \over \rho}{ {p_{i+1}^n - p_{i-1}^n} \over {2 \Delta x}} + \nu{{u_{i+1}^{n} -2u_i^n + u_{i-1}^{n}} \over {\Delta x^2}}\]
../_images/collocated.png

1.1.4.2.2. Apply Pressure Correction Approach

  • Split the N-S Equations into two parts

  • Step One: Ignore pressure gradient in momentum equation for intermediate velocity (\(u^*\) is not divergence free). From Equation (4):

(5)\[{{u_{i}^{*} - u_{i}^{n}} \over {\Delta t}} + {({u_{i+1}^{n})^2 - (u_{i-1}^{n})^2} \over {2 \Delta x}} = - \nu{{u_{i+1}^{n} -2u_i^n + u_{i-1}^{n}} \over {\Delta x^2}}\]

  • Step Two: Use intermediate velocity and correct it with the pressure (pressure enforces continuity) to obtain \(u^{n+1}\). From Equation (4):

\[{{u_{i}^{n+1} - u_{i}^{*}} \over {\Delta t}} = - {1 \over \rho}{ {p_{i+1}^n - p_{i-1}^n} \over {2 \Delta x}}\]
(6)\[u_{i}^{n+1} = u_{i}^{*} - {\Delta t \over \rho}{ {p_{i+1}^n - p_{i-1}^n} \over {2 \Delta x}}\]

  • Step Three: Use pressure correction Equation (6) to satsfy continuity, i.e. Equation (3) (just replace i in LHS of (6) with i+1 or i-1 and correct RHS)

\[{1 \over {2 \Delta x}} \left[ \left({u_{i+1}^{*} - {\Delta t \over \rho}{ {p_{i+2}^n - p_{i}^n} \over {2 \Delta x}}} \right) - \left( {u_{i-1}^{*} - {\Delta t \over \rho}{ {p_{i}^n - p_{i-2}^n} \over {2 \Delta x}}} \right) \right] = 0\]

Re-arranging this gives a form of the Poisson Equation, that ensures continuity:

(7)\[{{p_{i+2}^n - 2p_{i}^n + p_{i-2}^n} \over {4 \Delta x^2}} = {{u_{i+1}^{*} - u_{i-1}^{*}} \over {2 \Delta x}} {\rho \over {\Delta t} }\]

This is similar to using FTCS on the divergence of the momentum equation and setting the divergence of velocity to zero, as shown in the Poisson Equation for pressure. The form here includes only the first term on the RHS of that complex expression.

1.1.4.2.3. Odd-Even Decoupling

Note:

  • The discretisation of pressure is on a \(2 \Delta x\) grid.

  • The discretisation of velocity is on a \(\Delta x\) grid.

In the final equation for \(p_i^n\) if the pressure used is at an even point on the grid, the velocity is at an odd point, this is called odd-even decoupling

\[p_{i}^n = {{p_{i+2}^n + p_{i-2}^n} \over {2}} - {{\Delta x \rho} \over {\Delta t}} ({u_{i+1}^{*} - u_{i-1}^{*}})\]

Possible drawback of odd-even decoupling:

The pressure at point \(i\) is not influence by the velocity component \(u_i^n\) and viceversa \(\Rightarrow\) can result in high-frequency oscillations.

  • Stencil for \(p\): \(\quad i-2, \qquad i, \qquad i+2\)

  • Stencil for \(u^*\): \(\ \ \qquad i-1, \quad i+1\)

1.1.4.2.4. Demonstration of Odd-Even Decoupling

For the cavity flow, using:

  • 41 x 41 mesh

  • dx = dy = 0.05

  • \(\nu\) = 0.01

  • Re = 200

Pressure is not monotonic due to odd-even decoupling

The stencil with the previous pressure correction method was:

  • Stencil for \(p\): \(\quad i-1, \qquad i, \ \qquad i+1\)

  • Stencil for \(u\): \(\quad i-1, \qquad \qquad \quad i+1\)

So the pressure at \(p_i\) is not influenced by \(u_i\)

(Source code, png, hires.png, pdf)

../_images/marker_and_cell_method-1.png

1.1.4.2.5. Solution to Odd-Even Decoupling

Define velocity and pressure on separate grids

  • Collocated grid (where odd-even decoupling took place):

../_images/collocated_2.png

  • Staggered grid (to prevent odd-even decoupling):

../_images/staggered.png

This solution was due to Harlow and Welch (1965)

What effect does this have on the discretised equations?

  • Continuity Equation written as:

(8)\[{{u_{i+{1 \over 2}}^{n+1} - u_{i-{1 \over 2}}^{n+1}} \over {\Delta x}} = 0\]

  • “Fractional step” or “pressure correction”

(9)\[{{u_{i+{1 \over 2}}^{n+1} - u_{i+{1 \over 2}}^{*}} \over {\Delta t}} = - {1 \over \rho}{ {p_{i+1}^n - p_{i}^n} \over {\Delta x}} +\]

As before, substitute (9) into (8)

(10)\[{{p_{i+1}^n - 2p_{i}^n + p_{i-1}^n} \over {\Delta x^2}} = {{u_{i+{1 \over 2}}^{*} - u_{i-{1 \over 2}}^{*}} \over {\Delta x}} {\rho \over {\Delta t} }\]

How do we obtain \({u_{i+{1 \over 2}}^{*}}\) etc ?

Answer: Averaging We get values at \(i+{1 \over 2}\) and \(i-{1 \over 2}\) by averaging adjacent values

This makes the equations fully coupled and eliminates odd-even decoupling

1.1.4.2.6. Extension of Staggered Grid to 2D

../_images/2D_staggered.png

This uses three independent grids:

  • One for \(p_{i,j}\) etc

  • One for \(u_{{i \pm {1 \over 2}}, {j}}\) etc

  • One for \(v_{i,{j \pm {1 \over 2}}}\) etc

Equations to be solved:

(11)\[{\partial u \over \partial x}+ {\partial v \over \partial y} = 0\]
(12)\[{\partial u \over \partial t} + {\partial u^2 \over \partial x}+ {\partial {uv} \over \partial y} = - {1 \over \rho} {\partial p \over \partial x} + \nu \left( {{\partial^2 u \over \partial x^2} +{ \partial^2 u \over \partial y^2} } \right) = - {\partial \psi \over \partial x} + \nu \left( {{\partial^2 u \over \partial x^2} +{ \partial^2 u \over \partial y^2} } \right)\]
(13)\[{\partial v \over \partial t} + {\partial vu \over \partial x}+ {\partial {v^2} \over \partial y} = - {\partial \psi \over \partial y} + \nu \left( {{\partial^2 v \over \partial x^2} +{ \partial^2 v \over \partial y^2} } \right)\]

\(\psi \Rightarrow\) pressure divided by density

Conversion from Conservative Form to Non-Conservative Form (to check equivalence) via product rule:

\[{\partial {uu} \over \partial x} + {\partial {uv} \over \partial y} = u {\partial u \over \partial x} + {\partial u \over \partial x}u + {\partial u \over \partial y}v + u{\partial {v} \over \partial y} = u \left( {\partial u \over \partial x} + {\partial v \over \partial y} \right)+ u {\partial u \over \partial x} + v {\partial u \over \partial y} = u {\partial u \over \partial x} + v {\partial u \over \partial y}\]

1.1.4.2.7. Application of Finite Difference Method to Staggered Grid

\[\left . {\partial u \over \partial t} \right |_{i+{1 \over 2},j}^n = {{u_{i+{1 \over 2},j}^{n+1} - u_{i+{1 \over 2},j}^{n}} \over {\Delta t}}\]
\[\left . {\partial u^2 \over \partial x} \right |_{i+{1 \over 2},j}^n = {{(u_{i,j}^n)^2 - (u_{i+1,j}^{n})^2} \over {\Delta x}}\]
\[\left . {\partial {uv} \over \partial y} \right |_{i+{1 \over 2},j}^n = { { (u_{i+{1 \over 2},j+{1 \over 2}}^n)(v_{i+{1 \over 2},j+{1 \over 2}}^n)- (u_{i+{1 \over 2},j-{1 \over 2}}^n)(v_{i+{1 \over 2},j-{1 \over 2}}^n)} \over {\Delta y} }\]
\[\left . {\partial \psi \over \partial x} \right |_{i+{1 \over 2},j}^n = {{(\psi_{i,j}^n) - (\psi_{i+1,j}^{n})} \over {\Delta x}}\]
\[\left . {\partial^2 u \over \partial x^2} \right |_{i+{1 \over 2},j}^n = {{u_{i+{3 \over 2},j}^n - 2u_{i+{1 \over 2},j}^n + u_{i-{1 \over 2},j}^{n}} \over {\Delta x^2}}\]

1.1.4.2.8. Where is the Velocity Known?

Velocities \(u,v\) are known only at half mesh points - i.e. at mid points of vertical and horizontal cell edges.

  • Known at \(u_{i \pm {1 \over 2},j}\) and \(v_{i \pm {1 \over 2},j}\) etc

  • Unknown at \(u_{i,j}\) or \(u_{i \pm {1 \over 2},j \pm {1 \over 2}}\) etc

You need to average from the half mesh points

1.1.4.2.9. How do we get the Velocity at the Corners and Centre of the Cells?

  • The velocity is known at the midpoint of the cell edges

  • The velocity is unknown at the corners and centres of cells (e.g. points a, b, c and d)

../_images/2D_staggered_averages.png

So for example, if we wanted the following derivative:

\[\left . {\partial {uv} \over \partial y} \right |_{i+{1 \over 2},j}^n = { { (u_{i+{1 \over 2},j+{1 \over 2}}^n)(v_{i+{1 \over 2},j+{1 \over 2}}^n)- (u_{i+{1 \over 2},j-{1 \over 2}}^n)(v_{i+{1 \over 2},j-{1 \over 2}}^n)} \over {\Delta y} }\]

At Point a:

\[u_{i+{1 \over 2},j+{1 \over 2}}^n = {1 \over 2}({ u_{i+{1 \over 2},j+{1}}^n + u_{i+{1 \over 2},j}^n })\]
\[v_{i+{1 \over 2},j+{1 \over 2}}^n = {1 \over 2}({ v_{i+{1},j+{1 \over 2}}^n + v_{i,j+{1 \over 2}}^n })\]

Similarly for Point b

If we wanted to know this derivative:

\[\left . {\partial u^2 \over \partial x} \right |_{i+{1 \over 2},j}^n = {{(u_{i,j}^n)^2 - (u_{i+1,j}^{n})^2} \over {\Delta x}}\]

At Point c:

\[u_{i+1,j}^{n} = {1 \over 2}({ u_{i+{3 \over 2},j}^n + u_{i+{1 \over 2},j}^n })\]

At Point d:

\[u_{i,j}^n = {1 \over 2}({ u_{i+{1 \over 2},j}^n + u_{i-{1 \over 2},j}^n })\]

1.1.4.2.10. Historical Notes

Harlow and Welch (1965) introduced the “Marker and Cell” method:

  • It included marker particles to follow free surfaces (now obsolete)

  • Current usage of “Marker and Cell” method (MAC method) means - “Projection Method using a Staggered Grid”