1.1.3.1. Numerical Schemes 1

1.1.3.1.1. Setting the Scene: Stability

  • We encounter several instances when the solution “blows up”. Why?

  • Upwind schemes, implicit schemes, 2nd order schemes, leapfrog schemes

1.1.3.1.2. Consistency, stability and error analysis

Recall step one: 1D Linear Convection:

\[{\partial u \over \partial t} + c {\partial u \over \partial x} = 0\]

1.1.3.1.2.1. FD in time, BD in space

Explicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_i^n - u_{i-1}^n} \over \Delta x}=0\]

Explicit schemes:

  • Very simple and economical

  • Restrictions for stability

Implicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_i^{n+1} - u_{i-1}^{n+1}} \over \Delta x}=0\]

1.1.3.1.2.2. FD in time, CD in space

Explicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_{i+1}^n - u_{i-1}^n} \over {2 \Delta x}}=0\]

Implicit version: \(n=n+1\) in the CD scheme

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_{i+1}^{n+1} - u_{i-1}^{n+1}} \over {2 \Delta x}}=0\]

Results in linear system of equation with tridiagonal matrix

1.1.3.1.2.3. FD in time, FD in space

Explicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_{i+1}^n - u_{i}^n} \over {\Delta x}}=0\]

Implicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{u_{i+1}^{n+1} - u_{i}^{n+1}} \over {\Delta x}}=0\]

FD or BD in space and implicit versions are called first order upwind schemes for the convection equation.

1.1.3.1.2.4. FD in time, 2nd order BD in space

Explicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{3u_i^n - 4 u_{i-1}^n + u_{i-2}^n} \over {2 \Delta x}}=0\]

Implicit version:

\[{{u_i^{n+1} - u_i^n} \over {\Delta t}} + c {{3u_i^{n+1} - 4 u_{i-1}^{n+1} + u_{i-2}^{n+1}} \over {2 \Delta x}}=0\]

1.1.3.1.2.5. 2nd order CD in time, 2nd order CD in space

Explicit version: (Leapfrog scheme)

\[{{u_i^{n+1} - u_i^{n-1}} \over {2 \Delta t}} + c {{u_{i+1}^n - u_{i-1}^n} \over {2 \Delta x}}=0\]

Implicit version:

\[{{u_i^{n+1} - u_i^{n-1}} \over {2 \Delta t}} + c {{u_{i+1}^{n+1} - u_{i-1}^{n+1}} \over {2 \Delta x}}=0\]

1.1.3.1.3. Example

Recall step one: 1D Linear Convection:

\[{\partial u \over \partial t} + c {\partial u \over \partial x} = 0\]

With these initial conditions:

\[x \le 0.9 \Rightarrow u_0(x) = 0\]
\[0.9 \le x \le 1.0 \Rightarrow u_0(x) = 10(x-0.9)\]
\[1.0 \le x \le 1.1 \Rightarrow u_0(x) = 10(1.1-x)\]
\[x \ge 1.1 \Rightarrow u_0(x) = 0\]
def diffusion(nt, nx, tmax, xmax, sigma, method):
   """
   Returns the velocity field and distance for 2D diffusion
   """
   # Increments
   dt = tmax/(nt-1)
   dx = xmax/(nx-1)

   # Compute c (given sigma)
   c = sigma * dx / dt

   # Initialise data structures
   import numpy as np
   u = np.zeros((nx,nt))
   x = np.zeros(nx)

   # X Loop
   for i in range(0,nx):
      x[i] = i*dx

   # Boundary conditions
   u[0,:] = u[nx-1,:] = 0

   # Initial conditions
   for i in range(1,nx-1):
      if(0.9<=x[i] and x[i]<=1):
         u[i,0] = 10*(x[i]-0.9)
      elif(1<x[i] and x[i]<=1.1):
         u[i,0] = 10*(1.1-x[i])
      else:
         u[i,0] = 0

   # Loop
   for n in range(0,nt-1):
      for i in range(1,nx-1):
         if(method=='BD'):
            u[i,n+1] = u[i,n]-dt*c*( ( u[i,n]-u[i-1,n] ) /dx )
         elif(method=='CD'):
            u[i,n+1] = u[i,n]-dt*c*( ( u[i+1,n]-u[i-1,n] ) / (2*dx) )

   return u, x

def plot_diffusion(u,x,nt,title):
   """
   Plots the 1D velocity field
   """
   import matplotlib.pyplot as plt
   import matplotlib.cm as cm
   plt.figure()
   colour=iter(cm.rainbow(np.linspace(0,1,nt)))
   for n in range(0,nt,1):
      c=next(colour)
      plt.plot(x,u[:,n],c=c)
      plt.xlabel('x (m)')
      plt.ylabel('u (m/s)')
      plt.title(title)
      plt.show()

(Source code)

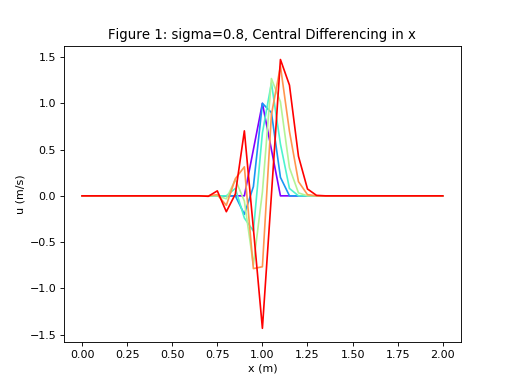
u,x = diffusion(6,41, 0.2, 2.0, 0.8, 'CD')
plot_diffusion(u,x,6,'Figure 1: sigma=0.8, Central Differencing in x')

u,x = diffusion(6,41, 0.2, 2.0, 0.8, 'BD')
plot_diffusion(u,x,6,'Figure 1: sigma=0.8, Backward Differencing in x')

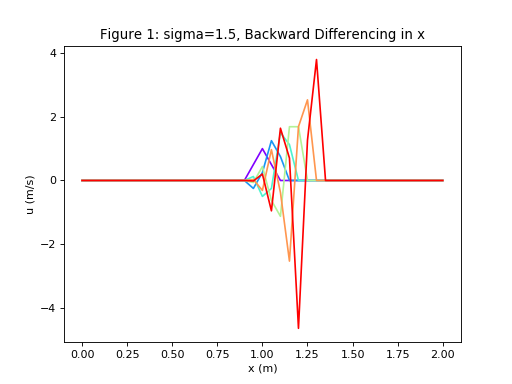
u,x = diffusion(6,41, 0.2, 2.0, 1.5, 'BD')
plot_diffusion(u,x,6,'Figure 1: sigma=1.5, Backward Differencing in x')

1.1.3.1.4. What Happened?

  1. Explicit CD scheme with the parameter \(\sigma = {{c \Delta t} \over {\Delta x}} = 0.8 \Rightarrow\) UNSTABLE

  2. 1st order upwind (Step 1) BD scheme \(\sigma = 0.8 \Rightarrow\) STABLE, but significantly diffused

  3. Do b) but with \(\sigma = 1.5 \Rightarrow\) UNSTABLE. This is conditional stability.

1.1.3.1.5. Basic Questions

  • What conditions should we impose on a numerical scheme to obtain an acceptable approximation to the problem?

  • Why do various schemes have such different behaviour?

  • How can we predict their stability?

  • For a stable scheme, how can we obtain information on the accuracy?

Need to define:

  • Consistency, Stability and Convergence

  • Truncation error - modified differential equation

  • Diffusion, Dispersion of the solution